Radioactive Decay Simulation
BACKGROUND
We have previously discussed radioactivity as the result of nuclear instability in lecture. Today, we will study the nature of radioactive decay. No matter which decay scheme (alpha, beta, gamma or some, more exotic, unmentioned schema) an unstable nucleus uses to rid itself of excess mass/energy, there is a certain probability that any unstable nuclei will decay in the next second. We call this probability the decay constant l. This probability is independent of how long the nucleus has already been in existence. The constant probability of undergoing radioactive decay leads to a form often seen in nature – exponential decay. The number of nuclei that will decay in a small time Dt is given by:
![]()
if N is large and l Dt is much less than 1. The number of nuclei remaining can be found by solving the equation for N as a function of time. Technically, we are solving a first order differential equation, but the answer is easy to find. First rearrange the equation to have all the N's on one side:
![]()
Next in the limit as Dt becomes small (i.e. ![]() ), we obtain:
), we obtain:
![]()
integrating both sides gives (don't worry if you haven't seen this in a math class):
![]() .
.
Next we exponentiate both sides of the equation to find
![]() .
.
The mathematics is made to agree with the physics by insisting that N(t) = the initial number of nuclei when t = 0. This number is called No.
![]()
The decay rate, or activity, is the number of nuclei that decay in a second. This is obtained by taking the negative of the derivative of N with respect to time:
![]()
The decay rate is the experimentally observed quantity. We detect nuclear decay by the emission of its alpha, beta, and/or gamma radiation.
Each radioactive material has a certain characteristic spectrum of its radiation. Although there is some overlap in spectral shapes, the decay constants are often sufficiently different to allow a determination of what kind of nucleus has decayed.
Often one speaks of the ‘half-life’ of a radioactive isotope. The half-life is the time required for a large number of nuclei to decay to one-half the original number. The activity also decreases to one-half of its initial value during a time of one half-life. The half-life is expressed as seconds, years, etc. If we have an isotope with a half-life of 100 seconds, and two nuclei of that species, one which was just created in a nuclear decay, and another which has already been in existence for 111 seconds, BOTH have the SAME probability of decaying during the next second -- namely 0.005! After 100 seconds each would have a probability of 0.5 of decaying.
Radioactivity experiments have fallen out of favor due to the possible exposure to minute amounts of activity. Hence some sort of simulation is often used. It is easy to cook up a computer program to simulate radioactive decay, However, it is satisfying to perform an actual experiment. We will do a simple experiment to acquire our data and then use Graphical Analysis to analyze it. As a simulation for the radioactive nuclei, we will use dice. When a one is showing on the top surface that die has decayed. If we think of the die as a nuclei, and a "roll" as a unit of time, then if we randomize the cubes well, the 1 has a probability of coming up one-sixth of the time for a six-sided die.
In nature, when one unstable nuclei decays, another of a differing half-life is often formed. The original unstable nuclei is called the parent, and the newly created unstable nuclei the daughter. By using dice with different numbers of sides, we can gain insight into how we can have around today radioactive isotopes with a half-life of a few hours. Surely in the 5 to 10 billion of years that has passed, almost all of the isotope would have decayed. The answer is that the short-lived isotopes are the daughter products of much longer-lived parents. The parents continuously decay, and at any time there is a nearly constant number of daughters (each of which quickly decays compared to the parent’s lifetime). Another possibility is a longer-lived daughter than the parent.
We can simulate the parent/daughter decay by including a die with a different number of sides for each of the parent decays. Using the same rule that a nucleus has decayed when its die turns up a one, we can track the decay dynamics as a function of time.
If one keeps track of the number of decay/birth events, the data obtained is called the activity – the number of decays per time interval. Our desire is to find the decay constant and/or the half-life of the decay by a number of means:
- Plotting ln(N) vs. t or ln(A) vs. t, one obtains a straight line of slope -l.
- Alternately, one can perform a non linear least squares fit to get a better result -- the logarithms can alter the slope somewhat.
- Another way to find the value of l is to calculate the approximate value of l for each interval and then perform an average and standard deviation. The approximate value of lambda for each interval is given by
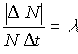
where N is the number of cubes before the roll.
- Other techniques include plotting N vs. t or A vs. t. Then, pick a starting value from the graph, and determine the time interval until the value is one half of the starting value. By repeating this with a large number of starting values, you can then find an average value for the half-life with a standard deviation. The half-life can be used to calculate the decay constant.
EXPERIMENTAL
Start with all of your parent dice in the pan. Randomize them by gently shaking and then pour them out on the table in a single layer. Remove every die that has a one showing on its top surface. Dice that are not setting flat should be re-randomized and then poured out as part of the same trial. Keep track of the number of decays of the parents, the total number of parents remaining, the number of daughters born, the number of daughters decaying and the total number of daughters. Assume that the births and decays take place simultaneously. Assume that each ‘roll’ is a time interval of 1 hour. Your activities will be in units of decays per hour. Continue the process until no die remains. Comment on any unexpected events that occurred while you were taking your data. You may find it useful to continue with the following table format. (If you set your table in Graphical Analysis, you can save some repetitive effort.) - Replace (N) with your initial number of parent dice.

Plot a graph of the data using Graphical Analysis. Make a column for each of the columns in your table. Look at the graph of the number of parent decays versus time and determine the approximate half-life of the decaying parent. Next, plot the number of parents remaining versus time. Print this graph and estimate its half-life. Compare the two half-lives. How well do they compare? From a statistical point of view, which, if either, do you feel is more reliable? Which looks more like a decaying exponential function? Which has more "noise"?
Now you should analyze your data and obtain the parent’s decay constant and the half-life by more sophisticated means. In fact, you use two different methods of analysis and compare the results. First, perform a nonlinear fit of the number of parent decays to the equation for A(t) given on the first page – print the graph when you have a good fit. Do not use the built in exponential fit! Type the equation on page 1except replacing A(t) with y. Calculate the half-life of the nuclei by using the fact that the half-life is given by:
![]()
Does your value for the half-life meet your expectations?
Next, have Graphical Analysis compute a new column that is the natural logarithm of the parent’s decay rate. Perform a linear fit on the logarithmic data. (You may want to refer to equation relating ln(N) to t on the previous page. Compare this value of l with the one you got from the first graph. Compare the initial activity by exponentiating the y-intercept of the linear graph and comparing that number with the nonlinear fit. Calculate a percentage error for A0 and
l. Next calculate the best fit initial number of nuclei (N0) by using the relationship between activity and number![]() .
.
Compare each value of the calculated initial number of nuclei to the true number that you started with. How well do they compare? Calculate a percentage error for each since you KNOW how many you started with.
Plot the number of daughter nuclei remaining versus time. Print this graph and include it with your report. Create a column of the log of the number of daughter nuclei remaining versus time. Plot this graph. Are there any straight segments? If so, select this range, and perform a linear fit to the straight segment. Determine the half-life of the daughter species.
Reflect upon what you have learned in this experiment in your summary.
Last Modified on January 09, 2008